What is Compound Interest: Definition, Formula, Examples, and Applications

Use Compound Interest Calculator

When people ask what is compound interest, they are really asking about one of the most powerful concepts in both mathematics and finance. Compound interest is the process by which interest is calculated not only on the original principal but also on the accumulated interest from previous periods. This means your money grows faster over time because you earn “interest on interest.” Understanding compound interest is essential for academic study in mathematics and economics, and it is equally critical for financial planning, investing, and debt management.

This comprehensive article will explain compound interest from both academic and financial perspectives. We’ll cover definitions, formulae, examples, comparisons, practical applications, and real-world insights.

Introduction to Interest

Interest is the cost of borrowing money or the reward for saving money. When you borrow from a bank, you pay interest. When you deposit money in a savings account, the bank pays you interest. The way this interest is calculated can significantly affect the total amount you pay or earn.

There are two main types of interest:

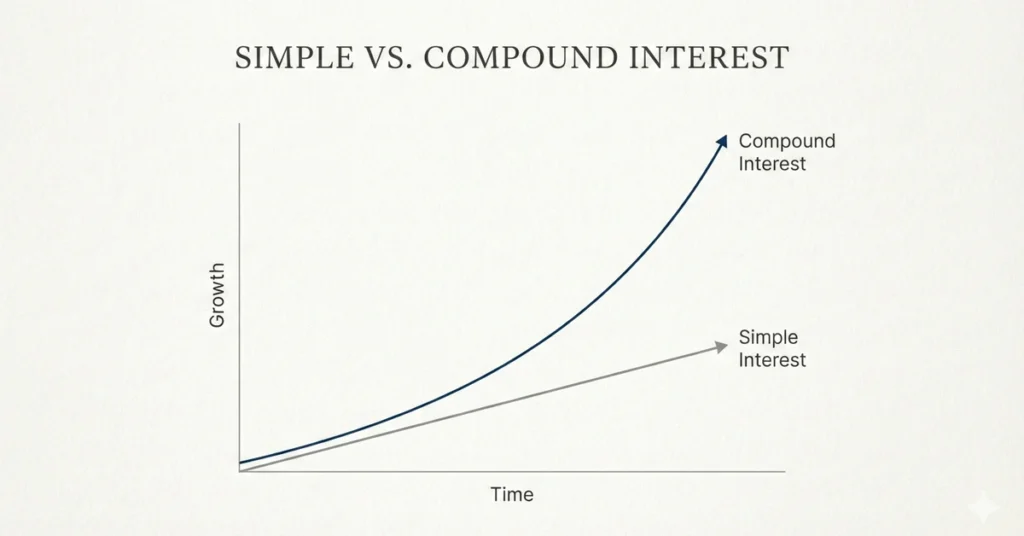
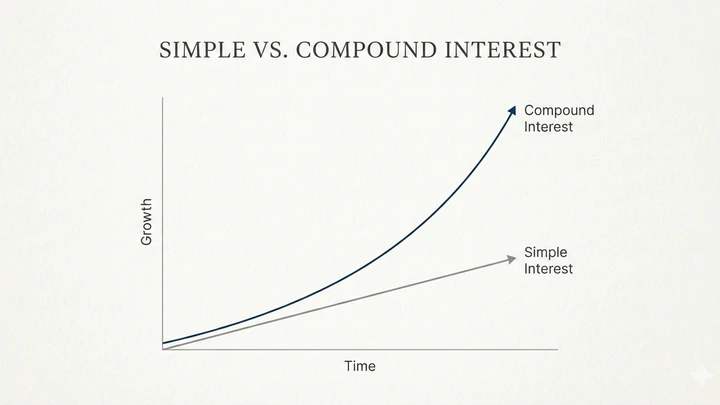
• Simple Interest: Calculated only on the principal.
• Compound Interest: Calculated on the principal plus accumulated interest.

Read Simple Interest vs Compound Interest Differences

What is Compound Interest: Definition

Compound interest is the addition of interest to the principal sum of a loan or deposit. It is the result of reinvesting interest, rather than paying it out, so that interest in the next period is earned on the principal plus previously accumulated interest.

Formula for Compound Interest:

$$A=P{(1+\frac{R}{n\times 100})}^{nT}$$

Where:

• $A$ = Total amount after time $T$
• $P$ = Principal (initial amount)
• $R$ = Annual interest rate (%)
• $n$ = Number of times interest is compounded per year
• $T$ = Time (in years)

Compound interest earned = $A-P$.

Watch Video Explanation

Academic Perspective: Why Students Study Compound Interest

In mathematics curricula, compound interest is introduced to help students understand:

• Exponential growth.
• Applications of percentages.
• Real-world financial literacy.

Students often solve problems like:

• “Find the compound interest on $5000 at 10% per annum compounded annually for 3 years.”
• “Find the compound interest on $5000 at 10% per annum compounded quarterly for 3 years.”

These problems illustrate how compounding frequency affects growth.

Financial Perspective: Why Compound Interest Matters

In finance, compound interest can mean the difference between modest savings and significant wealth.

• Loans: Borrowers face higher costs when interest compounds frequently.
• Investments: Investors benefit from compound interest because it accelerates growth.
• Savings Accounts: Banks use compound interest to attract customers.

Real-World Examples

Example 1: Compound Interest Investment

Suppose you invest $10,000 at 8% compound interest annually for 5 years.

$$A=10000\times (1+\frac{8}{100}{)}^5=10000\times (1.08{)}^5=14693$$

Compound interest = $14,693 – $10,000 = $4,693.

Example 2: Compound Interest Loan

Suppose you borrow $10,000 at 8% compound interest annually for 5 years. You will repay $14,693, which is $693 more than if the loan used simple interest.

The Power of Compounding

Albert Einstein reportedly called compound interest the “eighth wonder of the world.” The reason is that compounding can turn small investments into large sums over time.

Example: Investing $1,000 annually at 10% compound interest for 30 years results in over $164,000, compared to $30,000 invested.

Graphical Visualization

Practical Applications

• Car Loans: Often calculated using simple interest.
• Credit Cards: Use compound interest, which can quickly accumulate debt.
• Retirement Savings: Compound interest helps money grow exponentially over decades.
• Business Loans: May use either method depending on terms.

Insights: Compounding Frequency

The frequency of compounding matters:

• Annual compounding yields less than monthly compounding.
• Daily compounding yields the most growth.

Example: $1,000 at 10% for 1 year:

• Annual compounding = $1,100.
• Quarterly compounding = $1,103.81.
• Monthly compounding = $1,104.71.
• Daily compounding = $1,105.16.

Extended Academic Explanation

Why Compound Interest is Exponential

Each period, the interest is added to the principal, increasing the base for the next calculation. This recursive process leads to exponential growth.

Mathematical Proof

If interest is compounded annually:

$$A=P(1+R\mathrm{/}100{)}^T$$

This is a geometric progression, illustrating exponential growth.

Extended Financial Explanation

Mortgages

Mortgages use compound interest. Over 30 years, the total repayment can be double the principal.

Credit Cards

Credit cards compound interest daily. Missing payments can lead to rapid debt accumulation.

Investments

Mutual funds and stocks benefit from compound interest when dividends are reinvested.

Case Study: Retirement Savings

Suppose two people invest $5,000 annually at 7% compound interest.

• Person A starts at age 25.
• Person B starts at age 35.

By age 65:

• Person A has $1,068,000.
• Person B has $511,000.

Starting earlier makes a huge difference due to compounding.

Historical Context: What is Compound Interest in Early Finance

When historians ask what is compound interest, they trace it back to ancient civilizations. Mesopotamian merchants used simple interest in trade, but the idea of compounding emerged later when reinvested profits were recognized as a way to accelerate growth. By the Renaissance, bankers in Italy and merchants across Europe were already applying compound interest to long-term loans, laying the foundation for modern financial systems.

Mathematical Derivations: What is Compound Interest Formula Proof

To understand what is compound interest academically, students often derive the formula.

• Start with principal $P$.
• After one year at rate $R$, amount = $P(1+R\mathrm{/}100)$.
• After two years, amount = $P(1+R\mathrm{/}100{)}^2$.
• After $T$ years, amount = $P(1+R\mathrm{/}100{)}^T$.

This geometric progression shows why compound interest is exponential, unlike simple interest.

Extended Real-World Comparisons

• Student Loans: Many education loans accrue simple interest during study but switch to compound interest after graduation.
• Microfinance: Rural lending often uses simple interest for predictability, but savings accounts rely on compounding.
• Corporate Bonds: Investors reinvest coupons, effectively earning compound interest.

These examples highlight how answering “what is compound interest” depends on context: borrowing vs investing.

Behavioral Finance Insight

Psychologically, people often underestimate the power of compounding. This is known as the “exponential growth bias.” Teaching what is compound interest helps correct this bias, enabling better savings and investment decisions.

Advanced Applications

• Engineering Economics: Compound interest is used in net present value and internal rate of return calculations.
• Insurance: Premiums and payouts often rely on compound interest assumptions.
• Government Bonds: Treasury bills may use simple interest, while long-term bonds rely on compounding.

Practical Tips

• For Borrowers: Avoid loans with frequent compounding to minimize costs.
• For Savers: Choose accounts with frequent compounding to maximize returns.
• Check Compounding Frequency: Monthly compounding yields more than annual compounding.
• Understand Terms: Always read loan or investment agreements carefully.

Conclusion

Understanding what is compound interest is vital for both academic learning and financial decision-making. Compound interest is powerful because it grows exponentially, benefiting savers and investors but costing borrowers more. By mastering this concept, students gain mathematical insight, and individuals gain financial literacy.

Key Takeaways

• Compound interest is calculated on principal plus accumulated interest.
• It grows exponentially, unlike simple interest.
• Compounding frequency affects growth.
• Borrowers should minimize compounding; investors should maximize it.

Frequently Asked Questions

Explore MORE ARTICLES