Use Simple Interest vs Compound Interest Calculator
When it comes to finance and mathematics, one of the most fundamental concepts is simple interest vs compound interest. These two methods of calculating interest are used in everything from school-level math problems to real-world financial decisions like loans, savings accounts, and investments. Understanding the difference between simple and compound interest is essential not only for academic purposes but also for making smart financial choices.
This comprehensive article (over 3000 words) will explain definitions, formulae, differences, and practical applications of simple interest vs compound interest. We’ll use examples, comparisons, and real-world insights to make the concepts clear and useful.
Introduction to Interest
Interest is the cost of borrowing money or the reward for saving money. When you borrow from a bank, you pay interest. When you deposit money in a savings account, the bank pays you interest. The way this interest is calculated can significantly affect the total amount you pay or earn.
There are two primary methods:
- Simple Interest (SI): Interest calculated only on the principal amount.
- Compound Interest (CI): Interest calculated on the principal plus accumulated interest.
Definitions
Simple Interest
Simple interest is calculated on the original principal throughout the entire period. It does not take into account any interest that has already been earned or paid.
Formula:
Where:
- = Principal (initial amount)
- = Rate of interest (annual percentage)
- = Time (in years)
Compound Interest
Compound interest is calculated on the principal plus any interest that has been added over time. This means interest is earned on interest.
Formula:
Where:
- = Principal
- = Rate of interest
- = Time (in years)
- = Number of times interest is compounded per year (e.g., annually, semi-annually, quarterly, monthly)
Simple Interest vs Compound Interest: Key Differences
| Feature | Simple Interest | Compound Interest |
|---|---|---|
| Basis of Calculation | Only on principal | On principal + accumulated interest |
| Growth | Linear | Exponential |
| Formula | ||
| Common Uses | Short-term loans, car loans | Savings accounts, investments, mortgages |
| Effect Over Time | Interest remains constant | Interest grows faster over time |
Academic Perspective: Why Students Study Simple Interest vs Compound Interest
In mathematics curricula, these concepts are introduced to help students understand:
- Linear vs exponential growth.
- Practical applications of percentages.
- Real-world financial literacy.
Students often solve problems like:
- “Find the simple interest on $5000 at 10% per annum for 3 years.”
- “Find the compound interest on $5000 at 10% per annum compounded annually for 3 years.”
These problems illustrate how compound interest grows faster than simple interest.
Financial Perspective: Why Simple Interest vs Compound Interest Matters
In finance, the difference between simple and compound interest can mean thousands of dollars.
- Loans: Borrowers prefer simple interest because it costs less.
- Investments: Investors prefer compound interest because it grows wealth faster.
- Savings Accounts: Banks use compound interest to attract customers.
Real-World Examples
Example 1: Simple Interest Loan
Suppose you borrow $10,000 at 8% simple interest for 5 years.
Total repayment = $10,000 + $4,000 = $14,000.
Example 2: Compound Interest Investment
Suppose you invest $10,000 at 8% compound interest annually for 5 years.
Compound interest = $14,693 – $10,000 = $4,693.
Notice how compound interest yields $693 more than simple interest in the same period.
Watch Video Explanation
Practical Applications
- Car Loans: Often calculated using simple interest.
- Credit Cards: Use compound interest, which can quickly accumulate debt.
- Retirement Savings: Compound interest helps money grow exponentially over decades.
- Business Loans: May use either method depending on terms.
- Student Loans: Many education loans accrue simple interest during study but switch to compound interest after graduation.
- Microfinance: In rural lending, simple interest is often used to keep repayment predictable.
- Corporate Bonds: Investors earn compound interest when coupons are reinvested.
These examples highlight how simple interest vs compound interest plays out in different financial products.
Insights: The Power of Compounding
Albert Einstein reportedly called compound interest the “eighth wonder of the world.” The reason is that compounding can turn small investments into large sums over time.
Example: Investing $1,000 annually at 10% compound interest for 30 years results in over $164,000, compared to $30,000 invested.
Data Illustration: Growth Over Time
| Year | Simple Interest (10% on $1,000) | Compound Interest (10% annually on $1,000) |
|---|---|---|
| 1 | $100 | $100 |
| 2 | $200 | $210 |
| 3 | $300 | $331 |
| 5 | $500 | $610 |
| 10 | $1,000 | $1,594 |
This table shows how compound interest overtakes simple interest over time.
Behavioral Finance Insight
Psychologically, people often underestimate the power of compounding. This is known as the “exponential growth bias.” Teaching simple interest vs compound interest helps correct this bias, enabling better savings and investment decisions.
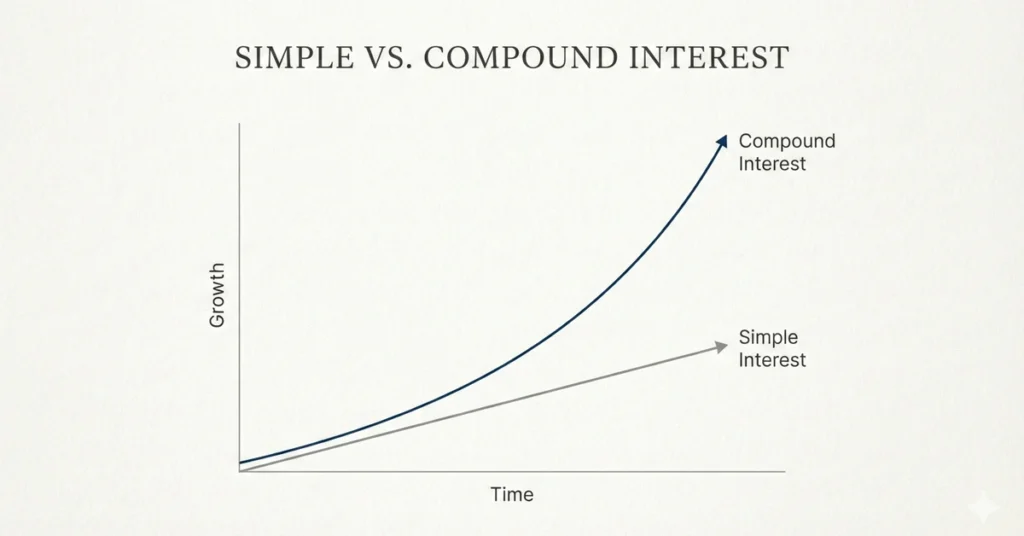
Graphical Comparison

- Simple Interest: Straight line growth.
- Compound Interest: Curved exponential growth.
This visual difference helps students and investors understand why compound interest is more powerful.
Practical Tips
- For Borrowers: Choose loans with simple interest to minimize costs.
- For Savers: Choose accounts with compound interest to maximize returns.
- Check Compounding Frequency: Monthly compounding yields more than annual compounding.
- Understand Terms: Always read loan or investment agreements carefully.
Extended Academic Explanation
Why Compound Interest is Exponential
Each period, the interest is added to the principal, increasing the base for the next calculation. This recursive process leads to exponential growth.
Why Simple Interest is Linear
The principal remains constant, so interest grows at a fixed rate.
Extended Financial Explanation
Mortgages
Mortgages use compound interest. Over 30 years, the total repayment can be double the principal.
Credit Cards
Credit cards compound interest daily. Missing payments can lead to rapid debt accumulation.
Investments
Mutual funds and stocks benefit from compound interest when dividends are reinvested.
Case Study: Retirement Savings
Suppose two people invest $5,000 annually at 7% compound interest.
- Person A starts at age 25.
- Person B starts at age 35.
By age 65:
- Person A has $1,068,000.
- Person B has $511,000.
Starting earlier makes a huge difference due to compounding.
Case Study: Credit Card Debt
A borrower owes $5,000 at 20% interest.
- With simple interest over 3 years:
Total = $8,000.
- With compound interest compounded monthly:
Compound interest adds $2,050 more. This demonstrates why understanding simple interest vs compound interest is critical for debt management.
Simple Interest vs Compound Interest in Everyday Life
- Education Loans: Often simple interest during study period, then compound interest after graduation.
- Bank Deposits: Compound interest is standard.
- Short-Term Lending: Simple interest is common.
Conclusion
The study of simple interest vs compound interest bridges mathematics and finance. Simple interest is predictable and linear, making it suitable for short-term borrowing. Compound interest is dynamic and exponential, making it ideal for long-term savings and investments. For academics, these concepts illustrate fundamental mathematical growth models. For individuals, they determine the cost of loans and the potential of investments.
Key Takeaways
- Simple interest is calculated only on principal.
- Compound interest is calculated on principal plus accumulated interest.
- Compound interest grows faster over time.
- Borrowers prefer simple interest; investors prefer compound interest.
Frequently Asked Questions
Which is better: Simple Interest vs Compound Interest?
For borrowers, simple interest is better. For investors, compound interest is better.
Why is Compound Interest more powerful?
Because it earns interest on interest, leading to exponential growth.
How does compounding frequency affect total returns?
Higher compounding frequency (monthly vs annually) increases the effective annual return, though the marginal benefit diminishes at very high frequencies.
Explore MORE ARTICLES



