Negative Exponents: To The Power Of Negatives

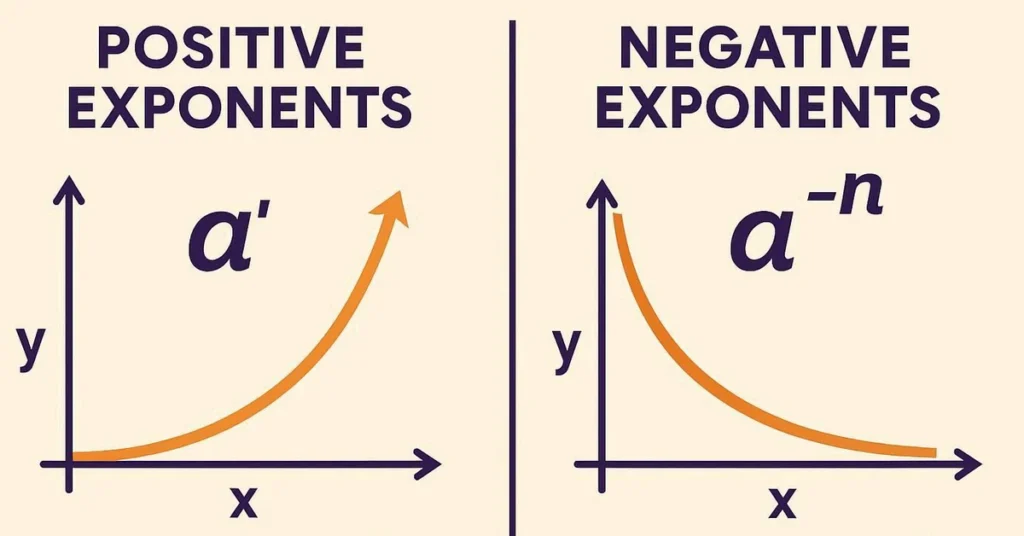
When students first encounter negative exponents or to the power of negative, it often feels counterintuitive. How can raising a number to a negative power produce a meaningful result? In reality, negative exponents are one of the most elegant tools in mathematics. They connect multiplication, division, and fractions into a unified framework. For academics, they illustrate the structure of algebra and exponential functions. For finance and science, they explain decay, discounting, and inverse relationships.

Introduction to Exponents

Exponents are one of the foundational concepts in mathematics, yet they often feel abstract until we see how they apply in real life. At their core, exponents are a shorthand way of expressing repeated multiplication. Instead of writing $2\times 2\times 2\times 2$, we can write $2^4$. This compact notation makes it easier to work with very large or very small numbers, and it also opens the door to deeper mathematical ideas like negative exponents, fractional exponents, and exponential growth or decay.

What Exponents Represent

• Repeated Multiplication: $a^n$ means multiplying the base $a$ by itself $n$ times.
• Scaling Numbers: Exponents can make numbers grow rapidly (positive exponents) or shrink quickly (negative exponents).
• Mathematical Consistency: Exponent rules unify multiplication, division, and reciprocals into one system.

Exponents represent repeated multiplication. For example:

• $2^3=2\times 2\times 2=8$.

But what happens when the exponent is negative?

• $2^{-3}=\frac{1}{2^3}=\frac{1}{8}$.

This simple rule — a negative exponent means “take the reciprocal” — unlocks a wide range of mathematical insights.

Negative Exponents vs Positive Exponents

Feature	Positive Exponents	Negative Exponents
Meaning	Repeated multiplication	Reciprocal of repeated multiplication
Growth	Expands	Shrinks
Applications	Compounding, growth	Discounting, decay

Exponents & To The Power Of: Definitions

Exponents are a compact way to express repeated multiplication or division. They allow us to represent very large or very small numbers with ease, and they form the foundation for understanding growth, decay, and reciprocal relationships. Let’s expand the definitions of positive exponents and negative exponents to make them clearer and more practical.

Positive Exponents

Definition:

$$a^n=a\times a\times a\dots (n\text{ times})$$

Where:

• $a$ = base
• $n$ = exponent (positive integer)

Examples:

• $2^3=2\times 2\times 2=8$
• $5^4=5\times 5\times 5\times 5=625$

Interpretation: Positive exponents represent growth or expansion. They are used in compounding interest, population growth, and scaling in science.

Negative Exponents

Definition:

$$a^{-n}=\frac{1}{a^n}$$

Where:

• $a$ = base
• $n$ = exponent (positive integer)

Examples:

• $2^{-3}=\frac{1}{2^3}=\frac{1}{8}$
• ${10}^{-2}=\frac{1}{{10}^2}=\frac{1}{100}=0.01$

Interpretation: Negative exponents represent reciprocals. Instead of multiplying, they shrink values by flipping the base. This is essential in discounting (finance), decay (science), and inverse-square laws (physics).

Zero Exponent

Definition:

$$a^0=1\text{(for any non-zero base)}$$

Example:

• $7^0=1$
• $(100{)}^0=1$

Interpretation: The zero exponent ensures consistency in exponent rules. It represents a neutral state between growth (positive exponents) and reciprocal shrinkage (negative exponents).

Reciprocal Relationship

One of the most important insights about negative exponents is the reciprocal relationship. A negative exponent doesn’t mean the number becomes negative — instead, it means the base moves to the denominator of a fraction.

For example:

$$5^{-2}=\frac{1}{5^2}=\frac{1}{25}$$

Here, the negative exponent simply tells us to “flip” the base. If the base is in the numerator, it moves to the denominator. If the base is already in the denominator, it moves to the numerator.

Another example with fractions:

$${\left(\frac{1}{3}\right)}^{-2}={\left(\frac{3}{1}\right)}^2=9$$

This shows that applying a negative exponent to a fraction inverts it first, then applies the positive exponent.

Practice Question

Question: Simplify the following expression using the reciprocal relationship of negative exponents:

$$\frac{2^{-3}\times 4^{-1}}{(5^{-2})}$$

Hint: Rewrite each negative exponent as a reciprocal, then simplify step by step.

Financial Discounting with Negative Exponents

One of the most powerful uses of negative exponents is in financial discounting. Discounting is the process of calculating the present value of money that will be received in the future. Instead of compounding forward with positive exponents, we move backward in time using negative exponents.

For example:

$$PV=FV\times (1+r{)}^{-t}$$

Here:

• $FV$ = Future Value
• $r$ = Interest rate per period
• $t$ = Number of periods
• The negative exponent $(-t)$ tells us to divide by the compounding factor instead of multiplying.

Worked Example: Suppose you expect $5,000 in 4 years, with an interest rate of 6%.

$$PV=5000\times (1.06{)}^{-4}=5000\times \frac{1}{1.262}=3962$$

So $5,000 in 4 years is worth $3,962 today.

Scientific Decay with Negative Exponents

Negative exponents are central to modeling scientific decay. In physics, chemistry, and biology, many processes decrease over time — such as radioactive decay, cooling, or population decline. The mathematics of decay uses exponential functions with negative exponents to show how values shrink instead of grow.

General Formula:

$$N(t)=N_0\times e^{-kt}$$

Where:

• $N(t)$ = amount remaining after time $t$
• $N_0$ = initial amount
• $k$ = decay constant
• The negative exponent $-kt$ ensures the value decreases over time.

Worked Example: Suppose a radioactive isotope has a half-life of 10 years. If you start with 100 grams, how much remains after 30 years?

$$N(t)=100\times {\left(\frac{1}{2}\right)}^{\frac{30}{10}}=100\times {\left(\frac{1}{2}\right)}^3=100\times \frac{1}{8}=12.5$$

So only 12.5 grams remain after 30 years. The negative exponent here models the repeated halving process.

Learn more about Exponential Functions in Science

Graphical Insight

• Positive exponents: exponential growth curve.
• Negative exponents: exponential decay curve.

Why Negative Exponents Work

Negative exponents are not a separate rule but a logical extension of the existing laws of exponents. They ensure consistency across all cases, including multiplication, division, and zero exponents.

Key Rule:

$$a^m\times a^n=a^{m+n}$$

If we let $m=2$ and $n=-2$:

$$a^2\times a^{-2}=a^{2-2}=a^0=1$$

This only makes sense if $a^{-2}=\frac{1}{a^2}$. In other words, negative exponents are required to preserve the balance of exponent rules.

Worked Example:

$$\frac{a^3}{a^5}=a^{3-5}=a^{-2}=\frac{1}{a^2}$$

Here, the negative exponent naturally emerges from division. Instead of inventing a new rule, we interpret $a^{-2}$ as the reciprocal of $a^2$.

Extended Financial Explanation

Discounting vs Compounding

• Compounding: $FV=PV\times (1+r{)}^t$.
• Discounting: $PV=FV\times (1+r{)}^{-t}$.

Negative exponents make discounting possible.

Case Study: Loan Repayments

Negative exponents are not just abstract math — they play a direct role in loan repayment calculations. When banks or financial institutions calculate the present value of future loan payments, they use discounting formulas that rely on negative exponents.

General Formula for Present Value of Loan Payments:

$$PV=\frac{PMT}{(1+r{)}^1}+\frac{PMT}{(1+r{)}^2}+\cdots +\frac{PMT}{(1+r{)}^t}$$

This can also be expressed compactly using negative exponents:

$$PV=PMT\times \left(\frac{1-(1+r{)}^{-t}}{r}\right)$$

Here:

• $PMT$ = periodic payment
• $r$ = interest rate per period
• $t$ = number of periods
• The term $(1+r{)}^{-t}$ is the negative exponent that discounts future payments back to today.

Worked Example: Suppose you borrow $10,000 at 8% annual interest for 5 years, with equal annual repayments.

Using the formula:

$$PMT=\frac{PV\times r}{1-(1+r{)}^{-t}}$$

$$PMT=\frac{10000\times 0.08}{1-(1.08{)}^{-5}}$$

Step 1: Calculate the negative exponent.

$$(1.08{)}^{-5}=\frac{1}{(1.08{)}^5}=\frac{1}{1.469}=0.681$$

Step 2: Subtract from 1.

$$1-0.681=0.319$$

Step 3: Divide.

$$PMT=\frac{800}{0.319}=2508$$

So the borrower pays $2,508 each year for 5 years.

Practical Tips

• Always Rewrite as Reciprocals: When you see a negative exponent, immediately rewrite it as a reciprocal. For example, $7^{-2}=1\mathrm{/}{7}^2$. This makes complex expressions easier to simplify.
• Use Fraction Inversion for Clarity: If the base is already a fraction, invert it before applying the exponent. For example, $(\frac{2}{3}{)}^{-3}=(\frac{3}{2}{)}^3=27\mathrm{/}8$.
• Check Consistency with Exponent Rules: Apply the subtraction rule: $\frac{a^m}{a^n}=a^{m-n}$. If the result is negative, interpret it as a reciprocal. This prevents mistakes in algebraic simplification.
• Apply in Finance for Discounting: Recognize that present value formulas use negative exponents. For example, $PV=FV\times (1+r{)}^{-t}$. This shows how future money shrinks when valued today.
• Apply in Science for Decay: Negative exponents model decay processes. For instance, radioactive half-life uses $(1\mathrm{/}2{)}^{t\mathrm{/}\text{half-life}}$. Understanding this helps in physics and chemistry.
• Use in Calculus for Derivatives: Rewrite fractions with negative exponents to simplify differentiation. For example, $\frac{1}{x^3}=x^{-3}$. This makes applying power rules straightforward.
• Check Units in Physics: Inverse-square laws (gravity, light intensity) use negative exponents. For example, $F\propto r^{-2}$. Recognizing this helps interpret physical relationships.
• Practice with Real Numbers: Test with simple bases like 2 or 10. For example, ${10}^{-1}=0.1$, ${10}^{-2}=0.01$. This builds intuition for how values shrink.
• Avoid Common Mistakes:
• Don’t confuse negative exponents with negative numbers. $2^{-3}=1\mathrm{/}8$, not $-8$.
• Don’t forget to apply the exponent to the entire base, especially in parentheses.
• Leverage Technology: Use calculators or spreadsheets to experiment with negative exponents. In Excel, typing =2^-3 gives 0.125. This reinforces the reciprocal relationship.

Behavioral Insight: How Learners and Professionals Perceive Negative Exponents

Negative exponents often trigger a psychological barrier because they feel “counterintuitive.” Many learners expect exponents to always make numbers larger, so seeing them shrink values can cause confusion. Recognizing this mental bias is key to mastering negative exponents.

Common Behavioral Patterns

• Fear of Abstraction: Students often assume negative exponents mean “negative numbers,” leading to mistakes like writing $2^{-3}=-8$.
• Preference for Concrete Examples: Learners grasp the concept faster when shown real-world applications (finance, decay, reciprocal fractions) rather than abstract algebra.
• Overlooking Reciprocity: People tend to forget that negative exponents simply mean “flip the base.” This oversight causes errors in simplification.
• Anchoring Bias in Finance: Borrowers may misinterpret discounting formulas because they expect growth, not shrinkage. Negative exponents help correct this bias.

Why This Matters

• Academically: Understanding the behavioral challenge helps teachers design better explanations — starting with simple reciprocal examples before moving to abstract rules.
• Financially: Borrowers and investors must overcome the instinct that “future money is bigger” by recognizing that discounting (negative exponents) makes future money worth less today.
• Scientifically: In decay models, negative exponents explain why values decrease over time, countering the intuitive expectation of growth.

Practice Question

Question: Why does the expression ${10}^{-1}=0.1$ often confuse beginners, and how can the reciprocal relationship help overcome this misunderstanding?

Hint: Think about how learners expect exponents to increase values, and how rewriting ${10}^{-1}$ as $1\mathrm{/}10$ clarifies the concept.

Advanced Applications of Negative Exponents

Negative exponents are not limited to simple reciprocal calculations — they appear in advanced mathematics, finance, science, and engineering. Their versatility makes them a powerful tool across disciplines.

1. Calculus and Analysis

• Derivatives of Power Functions: Writing fractions as negative exponents simplifies differentiation. Example: $\frac{1}{x^3}=x^{-3}$. Derivative: $\frac{d}{dx}{x}^{-3}=-3x^{-4}$.
• Integration: Negative exponents help integrate rational functions. Example: $\int x^{-2}dx=-x^{-1}+C$.

2. Physics and Engineering

• Inverse-Square Laws: Gravity, light intensity, and electric fields use negative exponents. Example: $F\propto r^{-2}$.
• Signal Processing: Attenuation of signals over distance often modeled with negative exponents.
• Material Science: Stress-strain relationships sometimes involve inverse power laws.

3. Finance and Economics

• Discounted Cash Flow (DCF): Negative exponents calculate present value of future cash flows. Example: $PV=FV\times (1+r{)}^{-t}$.
• Bond Pricing: Coupon payments are discounted using negative exponents.
• Risk Models: Probability decay functions often use exponential terms with negative exponents.

4. Probability and Statistics

• Exponential Distribution: Models waiting times with negative exponents. Example: $f(x)=\lambda e^{-\lambda x}$.
• Decay of Probabilities: Negative exponents describe how likelihood decreases over time.

5. Computer Science

• Algorithm Complexity: Reciprocal relationships in performance scaling can be expressed with negative exponents.
• Machine Learning: Regularization terms sometimes use inverse power functions to penalize large coefficients.

6. Chemistry and Biology

• Radioactive Decay: Uses exponential functions with negative exponents.
• Population Models: Negative exponents describe decline in populations under certain conditions.
• Pharmacokinetics: Drug concentration in the bloodstream often modeled with exponential decay.

Practice Question

Question: A bond pays $1,000 annually for 5 years. The discount rate is 6%. Using negative exponents, calculate the present value of the bond.

Hint: Apply the annuity formula:

$$PV=PMT\times \frac{1-(1+r{)}^{-t}}{r}$$

Focus on simplifying the negative exponent term first.

Academic Perspective: Why Study Negative Exponents

Students study negative exponents to:

• Understand reciprocal relationships.
• Connect algebra to fractions.
• Explore exponential functions in both growth and decay.
• Prepare for calculus, finance, and physics applications.

Financial Perspective: Why Negative Exponents Matter

In finance, negative exponents appear in discounting formulas. For example:

$$PV=\frac{FV}{(1+r{)}^t}=FV\times (1+r{)}^{-t}$$

Here, the negative exponent reflects discounting — the inverse of compounding.

Conclusion

Negative exponents are more than just a mathematical curiosity — they are a bridge between growth and decay, compounding and discounting, multiplication and division. By understanding negative exponents, learners gain clarity on reciprocal relationships, while professionals unlock tools for finance, science, and engineering.

Academic Significance

• They ensure consistency in exponent rules, extending the logic of multiplication and division seamlessly.
• They prepare students for advanced topics like calculus, probability, and algebraic manipulation.

Financial Importance

• Negative exponents drive discounting formulas, allowing us to calculate present value and compare loans, investments, and bonds.
• They highlight the inverse relationship between compounding growth and discounting shrinkage.

Scientific Relevance

• Negative exponents model decay processes, from radioactive half-life to cooling laws.
• They underpin inverse-square laws in physics, explaining how forces and intensities diminish with distance.

Key Takeaways

• Negative exponents mean reciprocals, not negative numbers.
• They unify mathematical rules across positive, zero, and negative powers.
• They appear in real-world contexts: finance (discounting), science (decay), and physics (inverse-square laws).
• Mastery of negative exponents builds confidence in handling advanced applications.

Final Thought

Negative exponents remind us that mathematics is not just about making numbers bigger — it’s about balance. Every growth has a decay, every compounding has a discounting, and every multiplication has a reciprocal. By embracing negative exponents, we see the elegant symmetry of mathematics and its practical power in the real world.

Frequently Asked Questions

Explore MORE ARTICLES